LLM-Pruner
Background Knowledge
Pruning, 剪枝,顾名思义,就是移除大模型中不必要的参数或组件。
我觉得这种思想基于的假设是:不相信大模型中各参数都是独立同分布的,大模型应当是高维空间中的某种低维的流形,那么理论上大模型就不需要这么高维的表示。这也类似于传统深度学习中的 bottleneck 思想。
当前的大模型剪枝方式主要可以分为两种,非结构化剪枝和结构化剪枝。
- Unstructured Pruning: 非结构化剪枝的粒度是模型的参数。一般是通过 Mask 将重要性低于阈值的参数置零,得到不规则的稀疏结构。这种方式并不改变模型的结构,所以对性能的影响较小,但是正因如此,剪枝后的模型参数并没有减少,要体现剪枝的效果,必须依赖于专门针对稀疏结构的压缩技术和硬件,普适性较低。另外,模型的内存使用还是较高的。
- Structured Pruning: 结构化剪枝的粒度是模型的子结构。它会在不改变模型宏观结构的前提下,利用某种规则物理地移除网络中的子结构。这样做的好处是真的降低了模型的参数数量,而且不再依赖于特定的硬件。但因为粒度较粗,当剪枝比例提升时,会导致模型性能下降较快。
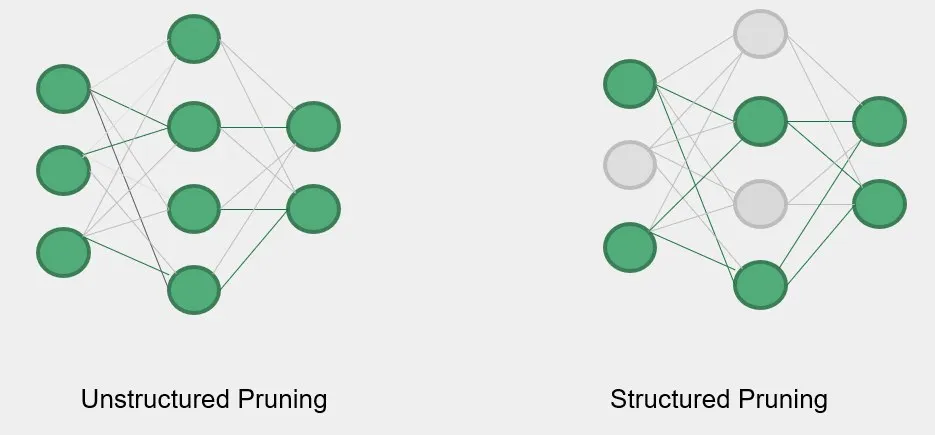
接下来要介绍的这篇文章使用的是结构化的剪枝。
Challenges
大模型的压缩主要有以下挑战:
- 模型规模越来越大,导致很多需要训练的压缩方案,比如知识蒸馏,变得很困难。
- 训练语料的限制,一方面,模型的原始训练语料一般不公开,另一方面,海量的训练语料需要高昂的收集成本,几乎是不可得的。
- 现有的大模型压缩算法往往针对单一、特定的任务,这导致大模型丢失了极为宝贵的处理通用任务的能力。
Motivation
因此,我们需要一种压缩方式,它无需大规模的训练,且能够维持大模型处理通用任务的能力。目前比较可行的方案是量化和剪枝,这两种方案的组合也确实能取得更好的模型压缩效果。这篇 paper 提出了一种结构化剪枝方法,能够实现以下这些目标:
- 压缩后的模型仍然能够处理通用任务。
- 只需要约 50k 的公开语料,用于压缩后调优训练。
- 较快的压缩效率,剪枝只需要 3 分钟,压缩后调优训练也只需要 3 小时。
- 能够自动完成剪枝,无需人工指导。
- 不需要像非结构化剪枝那样,依赖于特定的硬件。

Methods
Discover All Coupled Structure in LLMs
因为不同模型子结构之间是有着依赖关系的,不能简单的移除某些子结构就算了,这会导致模型的正确性出问题。
假设 \(N_i,N_j\) 为模型中的两个神经元,\(In(N_i),Out(N_i)\) 表示 \(N_i\) 输入输出所指向的所有神经元,\(Deg^-(N_i),Deg^+(N_i)\) 分别表示神经元 \(N_i\) 的入度和出度。
我们如下定义子结构之间的依赖。
第一种依赖是神经元 \(N_j\) 的输入只有 \(N_i\)。
\[N_j \in Out(N_i) \wedge Deg^-(N_j)=1 \Rightarrow N_j \text{ is dependent on }N_i\]
flowchart LR
i((i)) --> j((j))
i((i)) --> k((k))
l((l)) --> k((k))
第二种依赖是神经元 \(N_i\) 的输出只导向 \(N_j\)。
\[N_i \in In(N_j) \wedge Deg^+(N_i)=1 \Rightarrow N_i \text{ is dependent on }N_j\]
flowchart LR
i((i)) --> j((j))
l((l)) --> j((j))
l((l)) --> k((k))
如果某个神经元仅依赖于另一个神经元,而且所依赖的那个神经元被剪枝了,那么这个神经元本身也要被剪枝。
通过识别神经元之间的依赖关系,我们可以构建一个依赖关系图,然后据此找到模型中耦合的结构,称为组,以组为单位进行剪枝。
以 LLaMA 为例,如图所示,主要存在三种耦合的可能 1. MLP 内部的耦合。 2. Multi-head Attention(多头注意力)内部的耦合。 3. 整个网络中的维度耦合。
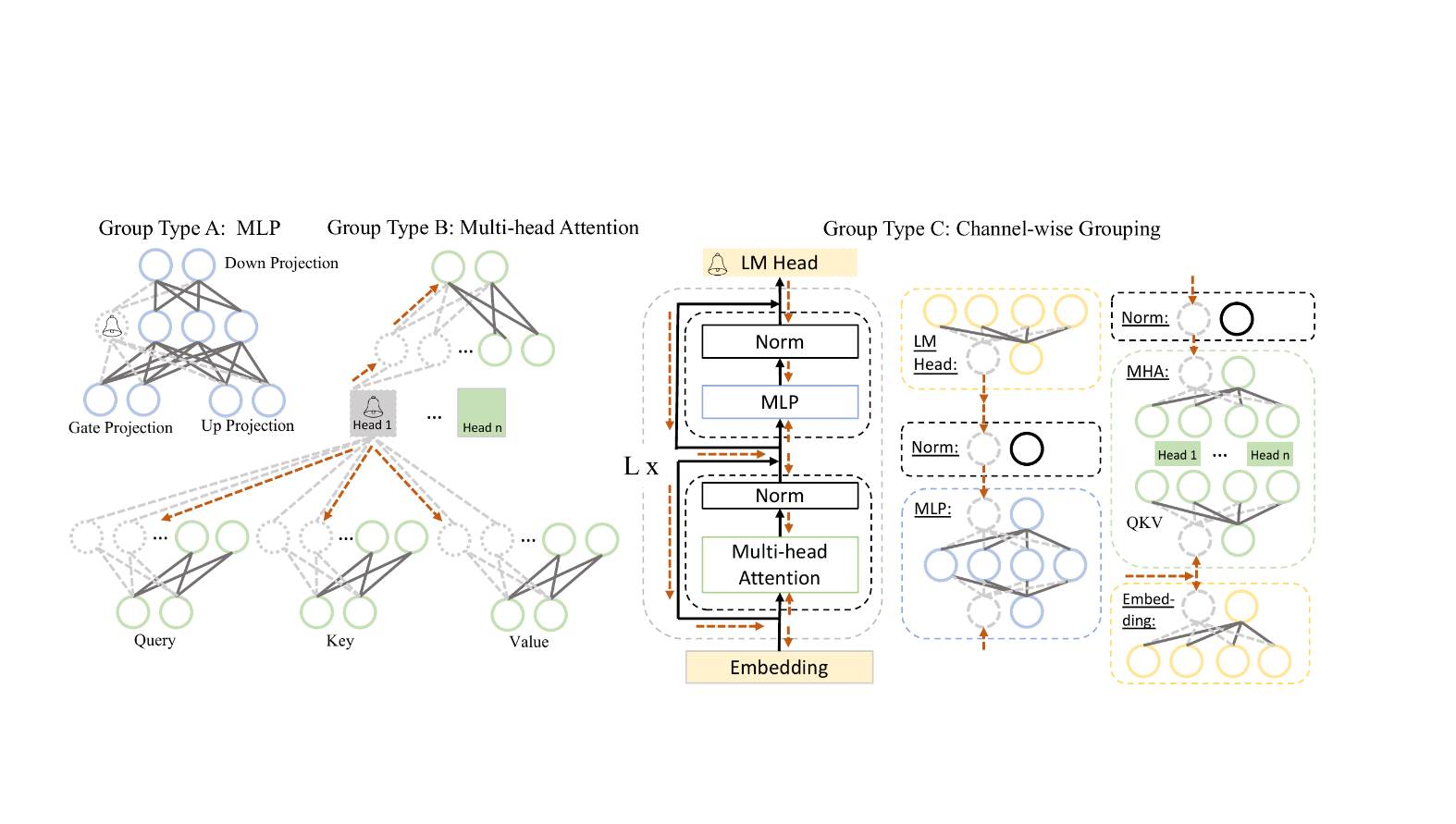
Grouped Importance Estimation
剪枝需要度量参数的重要性,然后才能去除不太重要的参数。
因为之前已经做过模型的依赖分析了,所以我们以组为单位评估重要性,而非以单个的神经元结构。
主要有两种度量方式。
Vector-wise Importance
第一,是以整个参数矩阵为单位,评估其重要性。
我们定义数据集 \(D=\{x_i,y_i\}_{i=1}^N\),在实验中使用 10 个样本就够了,这些样本主要来自于公共数据集。
一个组被定义为 \(\mathcal{G}=\{W_i\}_{i=1}^M\),\(W_i\) 是单个结构的参数,\(H\) 是 Hessian 矩阵。
那么一个参数矩阵的重要性,就可以度量为该矩阵起作用或不起作用对模型性能的影响,也就是模型的 Loss 与将模型中该参数矩阵置零的 Loss 之差。
\[I_{W_i} = | \Delta \mathcal{L}(\mathcal{D})| = |\mathcal{L}_{W_i}(\mathcal{D}) - \mathcal{L}_{W_i=0}(\mathcal{D})| =| \underbrace{\frac{\partial \mathcal{L}^{\top}(\mathcal{D})}{\partial W_i} W_i}_{\neq 0}-\frac{1}{2} {W_i}^{\top} H W_i + \mathcal{O}\left(\| W_i \|^3\right) | \]
此处还有一些小细节。 1. 因为使用的数据并不来源于模型的原始数据,所以模型在数据集上并未收敛,重要性的第一项不为零,使得可以较好地度量参数矩阵的重要性。 2. Hessian 矩阵的计算复杂度过高,所以只计算了对角线上的元素。
Element-wise Importance
除此之外,还可以度量更细粒度的重要性,比如单个参数的重要性。
其中 \(W_i^k\) 代表参数矩阵中的第 \(k\) 个参数,\(H_{kk}\) 是 Hessian 矩阵。计算重要性的思路跟前面讲的是一样的。
\[I_{W_i^k} = | \Delta \mathcal{L}(\mathcal{D})| = |\mathcal{L}_{W_i^k}(\mathcal{D}) - \mathcal{L}_{W_i^k=0}(\mathcal{D})| = | \frac{\partial \mathcal{L}(\mathcal{D})}{\partial W_i^k} W_i^k-\frac{1}{2} {W_i^k} H_{kk} W_i^k + \mathcal{O}\left(\| W_i^k \|^3\right) |\]
另外,还可以通过 Fisher Information Matrix 来近似 \(H_{kk}\) 的对角线,就不过多赘述了。
\[I_{W_i^k} = | \mathcal{L}_{W_i^k}(\mathcal{D}) - \mathcal{L}_{W_i^k=0}(\mathcal{D})| \approx | \frac{\partial \mathcal{L}(\mathcal{D})}{\partial W_i^k} W_i^k-\frac{1}{2} \sum_{j=1}^N \left(\frac{\partial \mathcal{L}(\mathcal{D}_j)}{\partial W_i^k} W_i^k\right)^2 + \mathcal{O}\left(\| W_i^k \|^3\right) |\]
Group Importance
拥有了上面的信息,我们就可以度量整个组的重要性了,文中给出了四种不同的方法,分别对应了不同的预设。
- Summation(求和): \(I_{\mathcal{G}} = \sum_{i=1}^{M}I_{W_i}\) or \(I_{\mathcal{G}} = \sum_{i=1}^{M}\sum_k I_{W_i^k}\),认为不同参数的重要性的独立可叠加的。
- Production(乘积): \(I_{\mathcal{G}} = \prod_{i=1}^{M}I_{W_i}\) or \(I_{\mathcal{G}} = \prod_{i=1}^{M}\sum_k I_{W_i^k}\),认为不同层的重要性会互相影响。
- Max(最大值): \(I_{\mathcal{G}} = \max_{i=1}^{M}I_{W_i}\) or \(I_{\mathcal{G}} = \max_{i=1}^{M}\sum_k I_{W_i^k}\),认为组的重要性由其中一层主导。
- Last-Only: \(I_{\mathcal{G}} = I_{W_l}\) or \(I_{\mathcal{G}} = \sum_k I_{W_l^k}\), \(l\) 是最后一层。认为组内的最后一层主导了整层的重要性,因为只有最后一层才会对后面的层产生影响。
我们可以更具不同的预设,使用不同的重要性度量方式,然后设置阈值,进行粒度为组的剪枝。
Fast Recovery with LoRA
在完成剪枝之后,需要对模型进行恢复训练,以提高模型的精度。这需要使用尽可能少的数据,并且尽可能地快,因此训练时需要使用尽可能少的模型参数。LoRA 正好能解决这一问题。
我们快速地过一遍 LoRA。
在 finetune 模型时,我们实际学习到的东西是 \(\Delta W\)。与 \(W_0\) 相比,\(\Delta W\) 并没有那么稠密的信息,所以我们可以假定 \(\Delta W\) 有低得多的内在维度,可以放心地进行降维。
因此,我们可以将矩阵 \(\Delta W\) 拆解为 \(BA\),其中
\[ B\in \mathbb{R}^{d\times r}, A\in \mathbb{R}^{r\times k},W\in \mathbb{R}^{d\times k}\] \[r \ll min(d,k)\]
在训练时,将 \(W_0\) 冻住,只计算 \(\Delta W=BA\) 的梯度更新。
\[W_{finetuned}=W_0+\Delta W=W_0+BA\]

因此,在训练时,我们可以只处理比原始大模型小得多的参数量,极大地提升了训练的速度。
现在,回到 LLM-Pruner。对于每一个可以训练的参数矩阵,我们都进行 LoRA finetune,以帮助模型恢复到剪枝前的水平。
\[f(x) = (W+\Delta W)X + b = (WX + b) + (PQ)X\]
Results
这篇文章对 LLaMA-7B, Vicuna-7B 和 ChatGLM 三种开源的大模型做了实验,得到了以下这些结论。
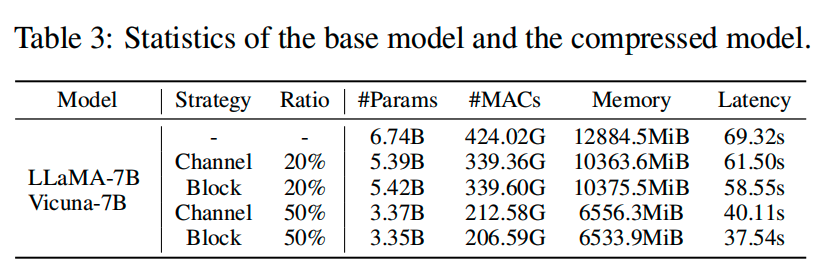
第一,剪枝降低了模型的参数量,提升了推理的速度。LLaMA-7B 原本只能在 24GB 的单卡上进行推理,剪枝后能 finetune 了。(表中的 Channel 和 Block 可以参照之前依赖计算时的分组策略)
第二,剪枝后模型仍然具备 Zero-shot 能力,能够处理通用的任务。
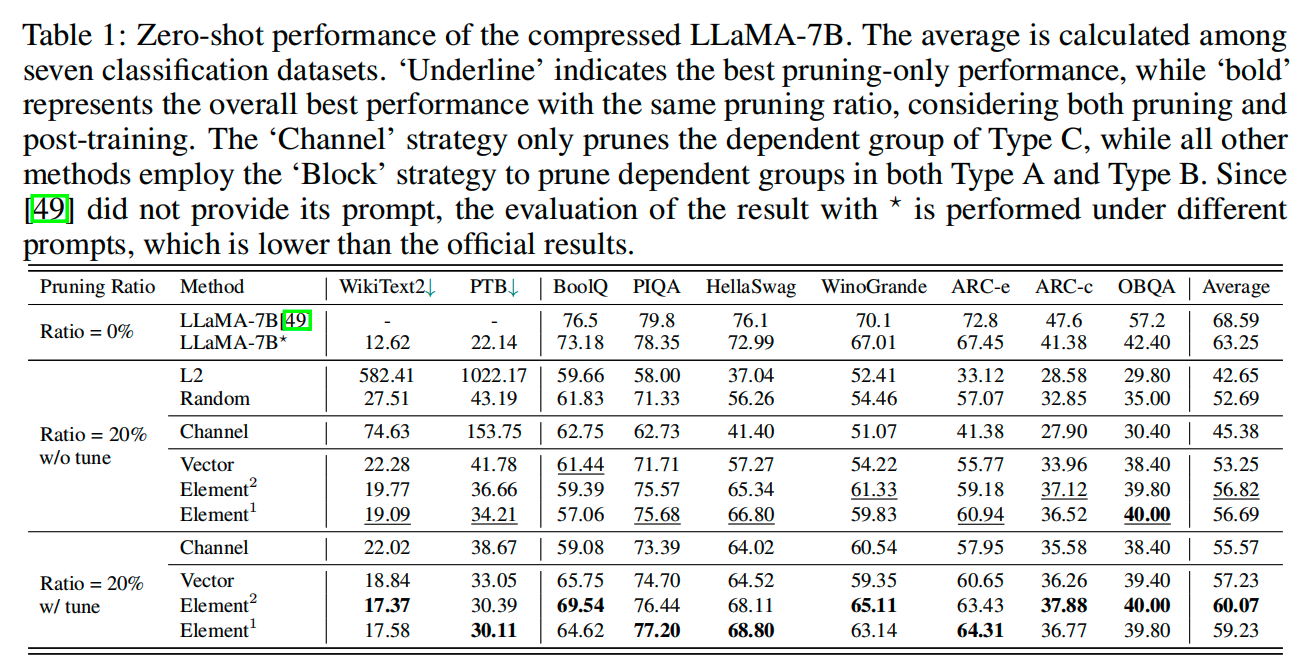
第三,相比与其他剪枝方法,比如 L2,LLM-Pruner 剪枝后的模型的性能更好。但是,当剪枝的比例增加时,还是会出现困惑度激增的情况,这有待研究。
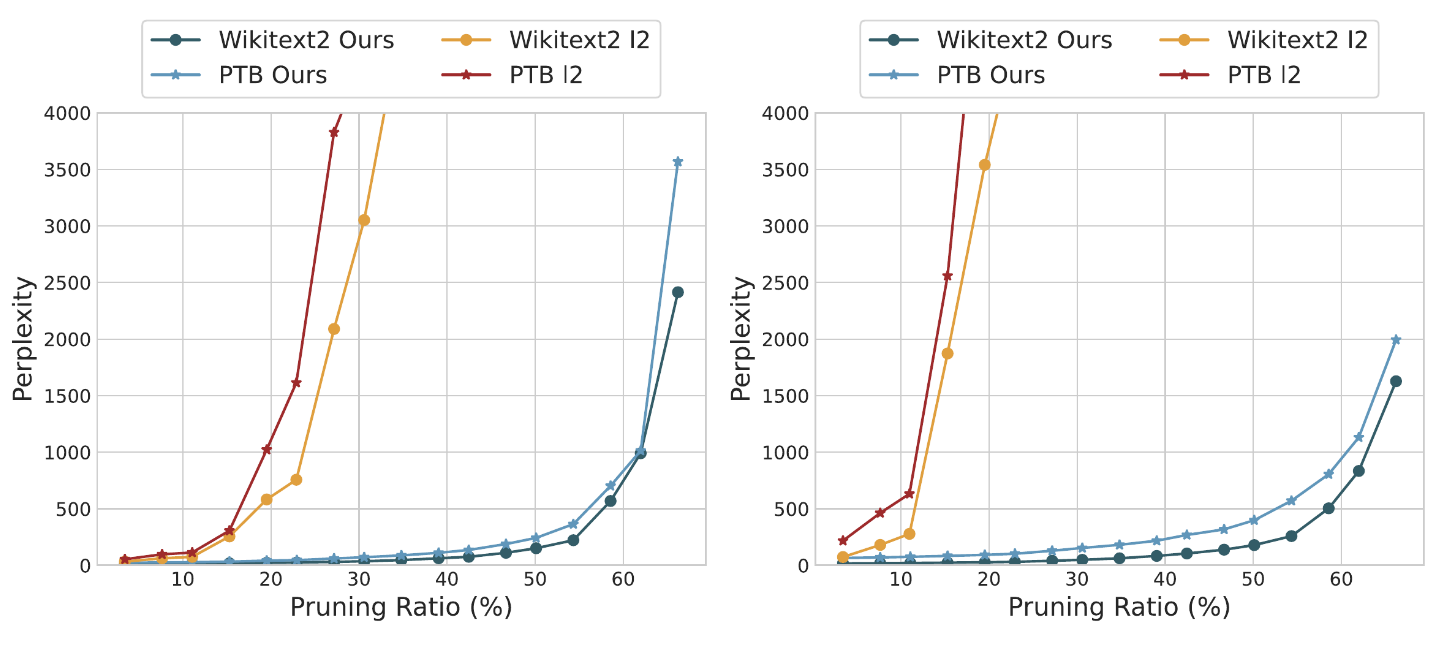
第四,通过一些例子,我们可以看到,剪枝后的模型仍然能够生成高质量的文本。

Reference
- LLM-Pruner:On the Structural Pruning of Large Language Models, https://arxiv.org/abs/2305.11627.
- LLM-Pruner Vedio&Slides, https://slideslive.com/39009677/llmpruner-on-the-structural-pruning-of-large-language-models.
- A Survey on Model Compression for Large Language Models, https://arxiv.org/abs/2308.07633.
- LoRA: Low-Rank Adaptation of Large Language Models, https://arxiv.org/abs/2106.09685.
- 大模型剪枝概述, https://zhuanlan.zhihu.com/p/691160917.
- LLM-Pruner: 大语言模型的结构化剪枝, https://zhuanlan.zhihu.com/p/630902012.