TensorGPT

发表于 分类于 阅读次数：
Efficient Compression of the Embedding Layer in LLMs based on the Tensor-Train Decomposition.

Background Knowledge

Low-Rank Factorization

低秩分解的思路和 LoRA 类似，只不过一个用于微调大模型，一个用于大模型压缩而已。

低秩分解将一个给定的大的参数矩阵 \(W\) 分解为两个小矩阵 \(U,V\)，其乘积近似于 \(W\)，从而降低参数量和计算开销。

\[W\approx UV\] \[U\in \mathbb{R}^{m\times k}, V\in \mathbb{R}^{k\times n}, k< min(m,n)\]

Token embedding

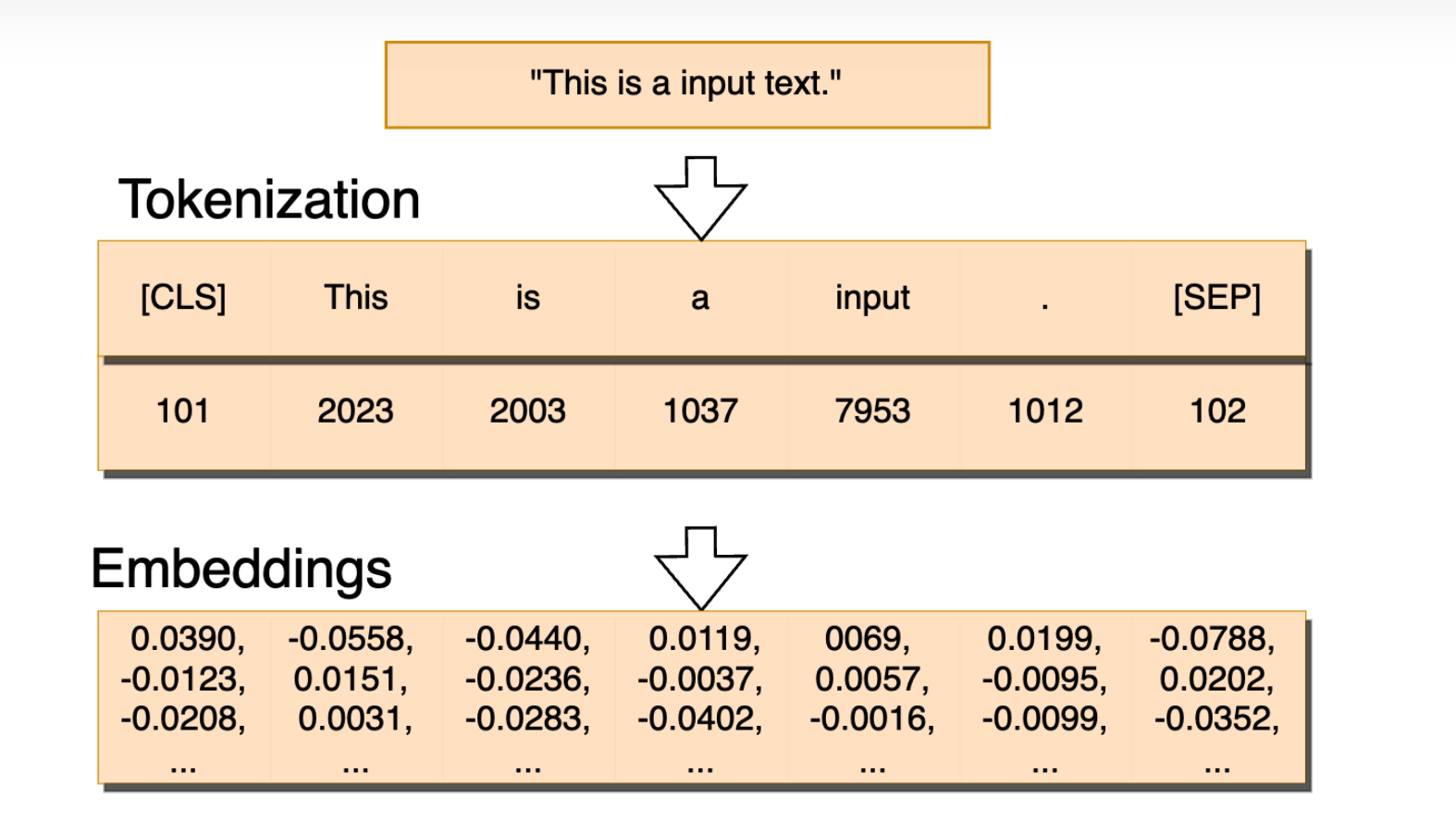
让我们回顾一下 embedding 的内容，首先，将一句话分词为一些 token，这些 token 转换成 one-hot 的 vector，然后通过 embedding 编码，将其映射为连续的词向量，用于接下来的推理和训练。我们可以将 embedding matrix 视作一个字典，one-hot vector 与之相乘，就是取出某一行的值，作为 token 对应的词向量。

为了捕捉微妙而复杂的语意，词向量的维度一般比较高，加之 token 的种类比较多，导致 embedding matrix 的参数数量过大，对存储和推理都造成了很大的障碍。

在 ELMo 之前，embedding 层一般是单独训练的，但是，在 ELMo 之后，很多模型会将 embedding 层与模型内部参数一起训练，所以对 embedding 层的压缩在一定程度上也能加速模型的训练或微调。

这篇文章主要探讨的是 embedding layer 的压缩，主要针对存储层面。

因为大模型的参数越来越多，规模越来越大，模型的存储成为了将大模型部署在轻量、低端设备上的主要障碍之一。

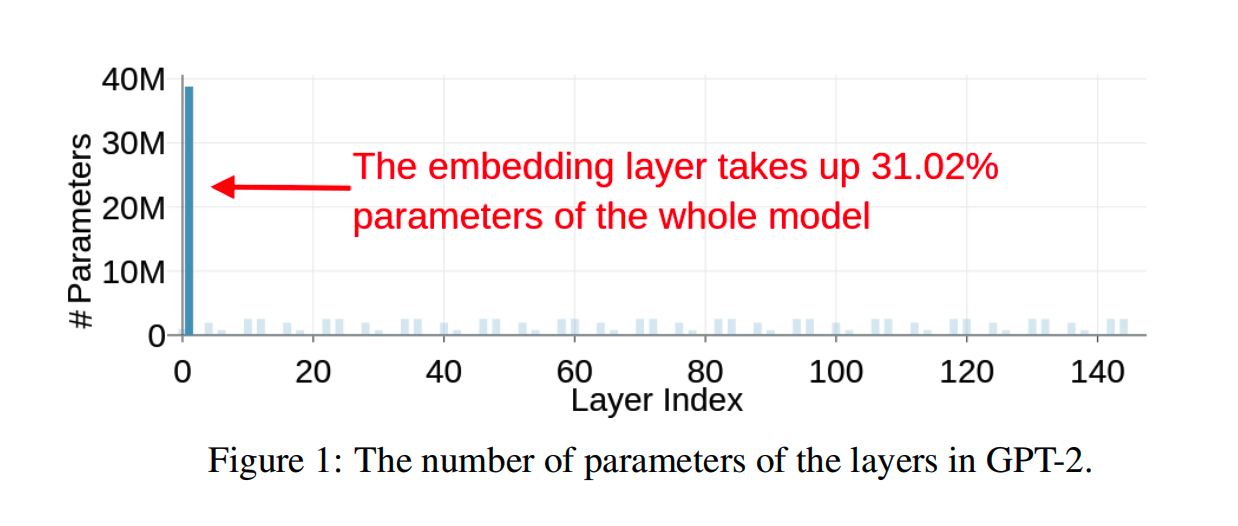
而提高存储效率的解决方案之一就是压缩 embedding layer。以 GPT-2 为例，如图所示，嵌入层占到了整个模型参数量的 31.02%。

Method

这篇文章的 Key Idea 很简单，就是将一个大的 Tensor 近似分解成一系列小的低秩 Tensor 的乘积。

分解的方法称之为 TTD，Tensor 分解后的表示形式称之为 MPS，矩阵乘积态。

具体的算法大概是先给定所有子 tensor 的维度，然后递归地对原始 tensor 做 SVD 分解，得到一系列子 Tensor。

具体的形式化表示如下：

\[\mathcal{X} \approx \mathcal{G}^{(1)} \times_2^1 \mathcal{G}^{(2)} \times_3^1 \mathcal{G}^{(3)} \times_3^1 \cdots \times_3^1 \mathcal{G}^{(N)}\]

\[\text{Original Tensor }\mathcal{X}\in \mathbb{R}^{I_1\times I_2\times...\times I_N}\] \[\text{Core Tensor }\mathcal{G}^{(n)}\in \mathbb{R}^{R_{n-1}\times I_n \times R_n}\] \[\text{Original Dimension }\{I_1,I_2,...,I_N\}\] \[\text{TT-rank }\{R_0,...,R_N\},R_0=R_N=1\]

但是，这种分解的粒度不应该是整个 embedding vocabulary，有两点原因：

  1. vocabulary 是频繁变动的，经常会添加一些 token vector，这时候如果是对整个 tensor 进行分解的话，每更改一次 vocabulary，就要重新运行一次分解算法。
  2. 分解算法的复杂度极高，如果分解整个 embedding vocabulay 的话要运行很久。

因此，本文提出了以 token 为粒度，对 embedding matrix 进行分解。因为 embedding matrix 本质上是一个字典，vocabulay 中的某行仅代表某个 token 的词向量，行与行之间没有依赖。因此，可以单独的对某一行进行分解。与之前讲的对应的，这样做有三点好处：

  1. 每次修改 embedding vocabulary，只要重新分解新增加的 token 对应词向量，而不用重新计算整个 tensor 的分解，计算完成后把结果 append 到原本的结果之后就行了。
  2. 因为行的分解是独立运算的，所以可以充分并行。
  3. 这也降低了存储开销，从 \(O(I^N)\) 降低到了 \(O(NR^2I)\)，这里假定 TTD-rank 和 Original Dimension 中的每个元素都是相等的。

另外，还有一些技术细节，譬如说，在对行向量进行 TTD 时，需要先将其 reshape 为 \(W^{2\times 2\times ... \times 2}\)，如果 \(W\) 的参数数量不是 2 的指数，将其补齐为 2 的指数，补齐的元素置零。

Results

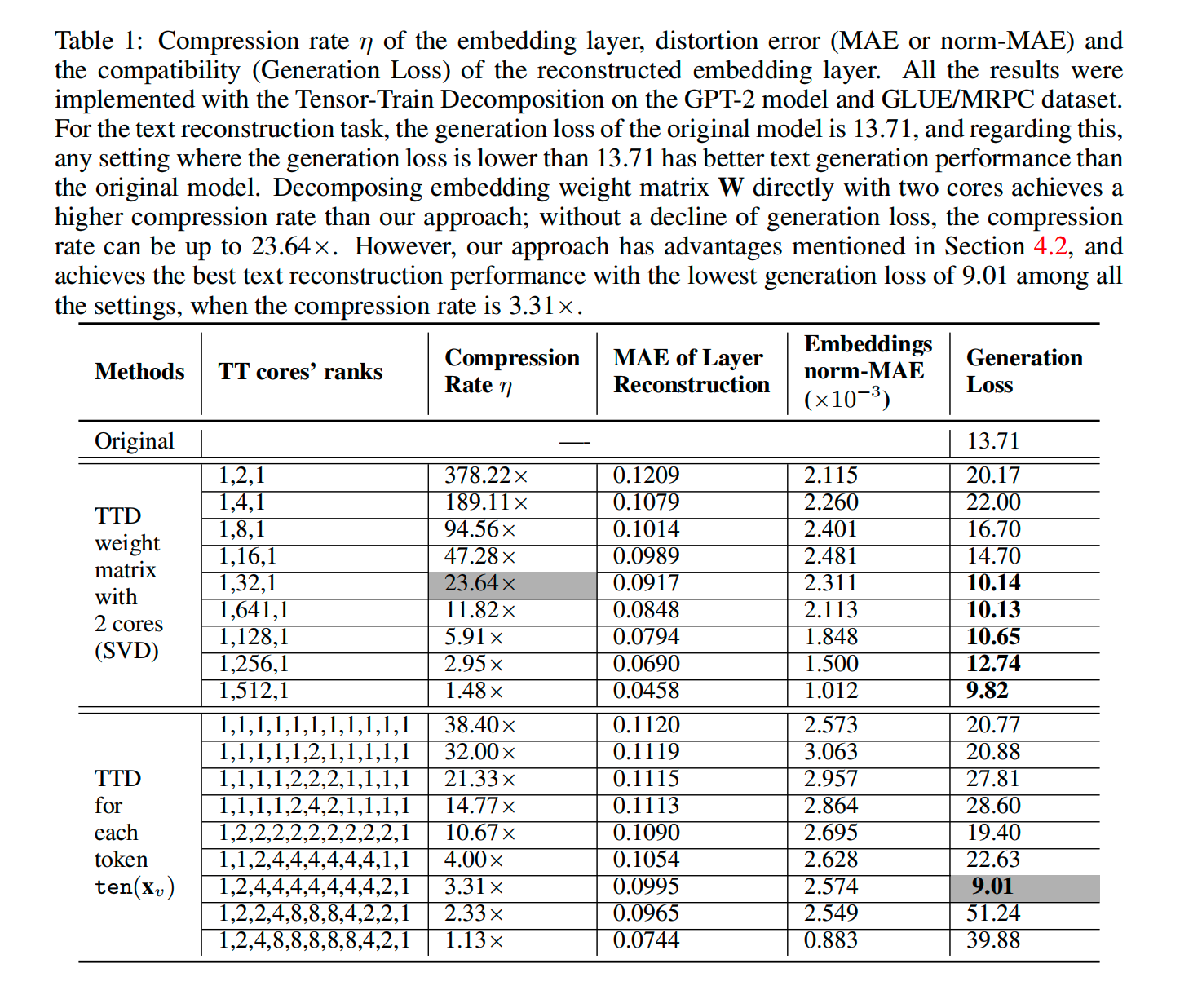
根据实验结果，可以看到， Embedding layer 最多压缩了 38.4 倍，而当压缩倍数时 3.31 时，甚至能产生比原始 GPT-2 模型更好的性能。

但是，这篇文章并没有考虑诸如位置编码等其他编码信息，而且并没有将 MPS 用于加速 token embedding 运算中，仅仅将其作为 embedding layer 的一种压缩表示。另外，文章只分析了 GPT-2，对于一片2023年的文章来讲多少有点陈旧了。

Reference

  1. TensorGPT: Efficient Compression of the Embedding Layer in LLMs based on the Tensor-Train Decomposition, https://arxiv.org/abs/2307.00526.
  2. A Survey on Model Compression for Large Language Models, https://arxiv.org/abs/2308.07633.